-$1 kitchen knife, 3Cr13/420, (very soft)
-Lum Chinese, VG-10, 59/60 HRC (Spyderco)
-k390, OTK 63/64 HRC (Peter's)
-s45,Kyle Bettleyon, M4 63 HRC
All knives have edge bevels of 6-8 dps, 15 dps micro-bevels with an x-coarse DMT. They were used to cut cardboard at a given speed/force and the sharpness measured by cutting light thread under a given load. I picked the x-coarse DMT because I had an idea that if the finish was very coarse then the apex would be thicker (you can see this in Verhoeven's work) and this might stabilize the carbides in the high carbide steels and increase the relative performance. However at the same time the coarse finish might lower the chip resistance that much that they chip out even though the apex is thicker. Hence do an experiment to find out which factor is larger and the resulting relative performance.
At the same time I wanted to check an idea I had for some time that the influence of cardboard itself is far greater than the knife steel. I normally random sample to prevent any bias from one knife seeing a different sample of cardboard than another. This time I didn't do that and so each knife on a particular run cut very different cardboard than another. Now to be clear it was all 1/8" ridged stock, all cut across the ridges. It was just different boxes used for each blade. I had seen from past results that cardboard can be extremely variable and easily 10:1 differences can be seen but I had never actually done a full run to measure its effect.
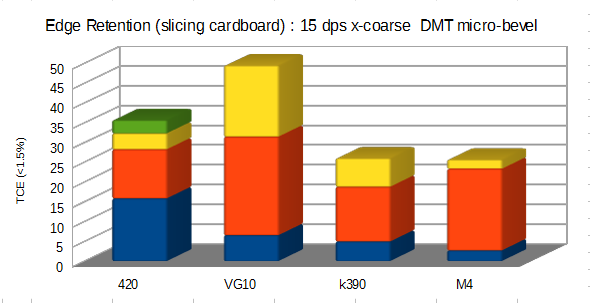
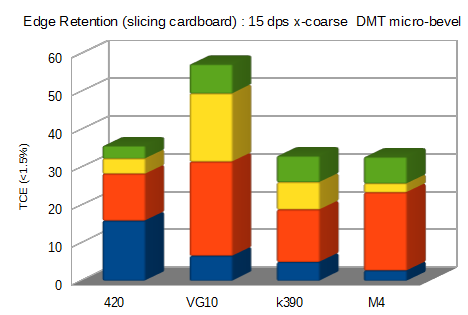
I tried a few charts to see the best way to look at the data, I think the stacked column shows two things clearly :
-the total edge retention of all runs added up
-each individual run (is color coded)
If you look at the results of one run with each (the blue one), it is almost the opposite of what you would expect from the steel as the 420J2 has the highest performance. However on the second run the high carbide blades catch up significantly, but on the third run some of the do but others fall back again.
In short, it shows clearly that even if you constrain everything very closely, the difference in cardboard -even of almost the same type visually- is so large than even looking at steels like 420 vs M4 you are not guaranteed to see consistent performance in the steel. All you do see, in regards to a difference, is which steel had the easiest cardboard to cut as the cardboard is making a much larger difference than the steel.
Now if you know a little statistics then you could wonder since this bias is just random it should normalize out, however I did a few calculations and since the cardboard variation is so high it looked like I would need at least 10 runs to even be able to say with confidence that there was a difference in the steels and even with ten runs I would not be guaranteed to see the actual correct steel influence.
I then did some monte carlo simulations to verify it and that was indeed the case. A monte carlo simulation is when you actually generate multiple data sets and look at how they compare with each other. For those curious the baselines are (1, 2, 2.5, 3 - this comes from other work on hemp/cardboard) and this is then each run modified by a random number from 1 to 10 representing the random nature of the cardboard. Here are three such simulated experiments :
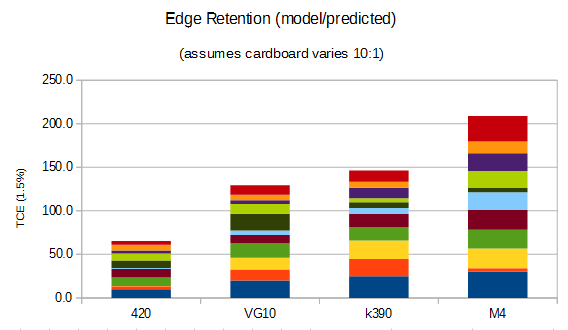
+

+
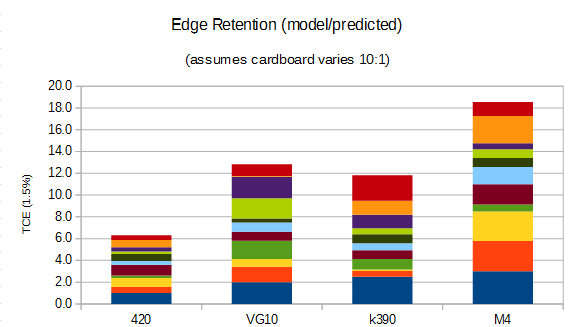
As predicted, even with 10 runs the most you would be able to conclude with confidence is that it isn't likely the steels have the same performance and that you might see a significant difference between something like 420 vs M2. However 10 runs isn't enough to determine the difference between something like VG-10 vs k390 vs M4.
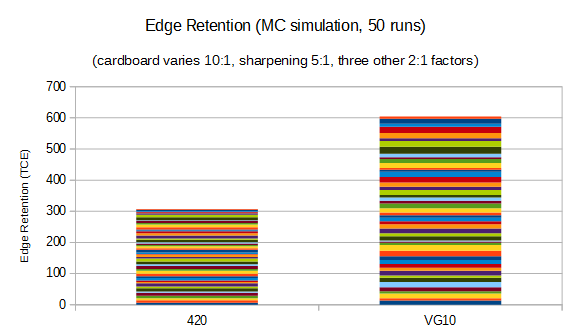
Now if you are a a little curious about statistics you might ask how big of a set you need and you can estimate it with a little calculations (a sum increases ~N, the error only increases ~root(n), this the larger the sample the smaller the percent error). It looked like 50 samples would in generate show the difference and again a MC simulation shows it to be likely :
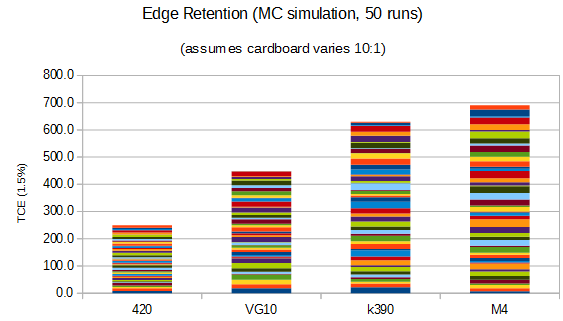
In short, if you are trying to do edge retention comparisons, and you don't heavily control the material cut, then it will take a LOT of work for the biases to randomize out and reveal the nature of the steel. If you are really curious, if I wanted to actually generate that chart on the bottom with physical data I would have to cut ~500 km of cardboard. I am not likely to do that, but I will at least do 5 runs and maybe 10.
If you think about this a little it should be obvious why we can also see huge differences in how different people experience steels. It is very likely that since people don't control materials in normal cutting, often what is seen as conclusions are just which steels tended to have the best luck in getting easy to cut cardboard. The unfortunate thing is that once that conclusion is formed it becomes self-reinforcing due to things like cognitive dissonance which causes conclusion bias. Hence the importance of things like at least partial blinding.
As a side note, if I had to pick a knife to use for this work it would be the OTK because the handle is the most comfortable in a hammer grip which is what is used for this work. Followed by a close second with the s45, a distant third with the Lum and I would never use the kitchen knife as it is too long and awkward and floppy on the stiffer cardboards.