Visualizing the Tradeoff of Higher Hardness

[xceptnl]

I posted this on Bladeforums a few days ago but I thought some of you might be interested in this as well. Many thanks to Larrin for doing all the hard work of testing steels and providing this data to the public. I just wanted to compile some of it in a different way.

This graph shows the effect of hardness on the toughness and edge retention of various steels:


(The numbers next to each steel are hardness values.)

Increasing hardness decreases toughness and increases edge retention as we all know. Larrin has shown that edge retention increases linearly with hardness, and at the same rate for most steels. This allowed me to predict edge retention where data was missing to produce this graph.

Toughness, on the other hand, does not show the same simple relationship with hardness. Tougher steels lose toughness very rapidly as you increase hardness without much increase in edge retention, while less tough steels benefit more from increased hardness. In mathematical terms, toughness decreases logarithmically with hardness. So making high-toughness steels harder seems to be a bad idea.

Some interesting things to note: Magnacut gets a good tradeoff at 62 RC and then falls off as you go harder. CPM-154 shows a better tradeoff than other steels near it. These may simply be the result of uncertainty in the data.

Again, thanks Larrin for giving us this data. I hope some of you find this useful in making decisions about steel and hardness.

Very interesting thread. Thanks for posting and for all who have contributed to the discussion. Learning something new each day.

[Bill1170]

I am fascinated to read that S60V (aka 440V) heat-treated by Shawn Houston could emerge from the dead with greatly improved performance.

[Synov]

I was trying to think of a way to visualize the effect of blade thickness and edge angle on toughness and edge retention at the same time.

A convenient mathematical relationship is that toughness is proportional to the cube of blade thickness, while edge retention is related both to the contact force at the blade tip and the thickness of the edge bevel: the larger the edge angle is, the thicker the edge bevel is, and the less contact pressure there is on the material being cut at the actual edge. As the edge wears away, contact pressure is reduced further until the blade ceases to cut.

Empirical data on edge angle and edge retention gives the relationship:

Edge Retention ∝ (sin(Edge Angle/2))^(-9/4)

If we reduce the blade thickness while keeping the bevel height the same, the bevel thickness decreases proportionally with blade thickness and we can get a simple relationship between toughness, edge retention and thickness.

Bevel Thickness ∝ sin(Edge Angle/2)
Edge Retention ∝ (Bevel Thickness)^(-9/4)
Edge Retention ∝ (Thickness)^(-9/4)

Since Toughness ∝ (Thickness)^3, we can use the results above to get the relationship:

Edge Retention ∝ (Toughness)^(-3/4)

And this can be visualized as such:



The dashed lines show the effect of reducing the blade/bevel thickness (and edge angle), confirming that edge angle can be even more important than the steel type.

[Mage7]

I was trying to think of a way to visualize the effect of blade thickness and edge angle on toughness and edge retention at the same time.

A convenient mathematical relationship is that toughness is proportional to the cube of blade thickness, while edge retention is related both to the contact force at the blade tip and the thickness of the edge bevel: the larger the edge angle is, the thicker the edge bevel is, and the less contact pressure there is on the material being cut at the actual edge. As the edge wears away, contact pressure is reduced further until the blade ceases to cut.

Empirical data on edge angle and edge retention gives the relationship:

Edge Retention ∝ (sin(Edge Angle/2))^(-9/4)

If we reduce the blade thickness while keeping the bevel height the same, the bevel thickness decreases proportionally with blade thickness and we can get a simple relationship between toughness, edge retention and thickness.

Bevel Thickness ∝ sin(Edge Angle/2)
Edge Retention ∝ (Bevel Thickness)^(-9/4)
Edge Retention ∝ (Thickness)^(-9/4)

Since Toughness ∝ (Thickness)^3, we can use the results above to get the relationship:

Edge Retention ∝ (Toughness)^(-3/4)

And this can be visualized as such:



The dashed lines show the effect of reducing the blade/bevel thickness (and edge angle), confirming that edge angle can be even more important than the steel type.

Interesting... Could this also be interpreted as a mathematical way to express edge stability? I kind of wonder how it might relate to how well an edge holds its front-end keenness since CATRA doesn't seem to measure that very much.

Just for clarification, you merely haven't graphed out the slope for AEB-L and 1V right?

[Synov]

Interesting... Could this also be interpreted as a mathematical way to express edge stability?

Edge stability is resistance to rolling and chipping, so it's not directly related to edge retention in the sense of abrasive edge wear. Edge stability is essentially the combination of toughness and hardness.

The relationship I'm talking about on the other hand is a combination of toughness and edge retention, mediated by the thickness of the steel. It doesn't take into account hardness, which is a bit more difficult to connect to everything else in a proportional way since the relationship of hardness and toughness is heavily dependent on the specific steel composition.

If you want to put a name to it you can call it the "balance" or "versatility" of the steel. This can be calculated as a metric for a particular steel at a particular hardness as (Edge Retention)(Toughness)^(3/4). 3V has the highest "balance" since its curve is the highest on the chart. Then if you combine this value with hardness in some way you have a nice way to compare the overall quality of different steels.

Just for clarification, you merely haven't graphed out the slope for AEB-L and 1V right?

1V and CruWear, as examples.

[horzuff]

I think conflating edge angle with stock or BTE thickness by arbitrarily assuming constant bevel height is confusing at best.

Why not just stick to edge angle which is the actual factor in question? Removes the weird, arbitrary layer of abstraction and is much more actionable by choosing edge angle as specified

[Synov]

I think conflating edge angle with stock or BTE thickness by arbitrarily assuming constant bevel height is confusing at best.

It's not arbitrary, it's necessary to maintain a proportional change in tougness. Also, the reduction in edge angle is pretty close to the reduction in thickness. For example, reducing the thickness of a blade throughout by 30% will reduce the edge angle by somewhere between 30% (for small angles) and 34% (large angles).

Why not just stick to edge angle which is the actual factor in question?

Because edge angle is not as easily correlated to toughness as blade thickness. How would you explain how the thickness of the blade would have to change as edge angle is reduced?

[horzuff]

Don't You think that's just forcing a relationship that's just not there? You can increase edge retention without decreasing toughness by decreasing edge angle while leaving thickness alone, or increase toughness without sacrificing edge retention by keeping the edge angle and increasing thickness.

There's just no real relationship between edge retention and blade cross section area unless You force this artificial constraint of constant bevel height. The only real factor is the primary bevel angle.

Additionally this ignores all other blade dimensions like height and secondary bevel angle which actually influence the cross section area and thus toughness.

This just makes this extrapolation misleading as it implies choosing a thinner knife will provide the user with better edge retention. It won't. Sharpening at a shallower angle will.

It would be much more informative to plot edge retention over edge angle - to help compare steels at their lowest sustainable edge angles

And much less useful, but still at least somewhat, plot toughness over thickness/cross section area as this can approximate which knives would meet our toughness requirements - to help compare overall toughness of particular knife models in given steels

[Synov]

Don't You think that's just forcing a relationship that's just not there? You can increase edge retention without decreasing toughness by decreasing edge angle while leaving thickness alone, or increase toughness without sacrificing edge retention by keeping the edge angle and increasing thickness.

Decreasing edge angle does decrease toughness, and increasing thickness does decrease edge retention or at least cutting ability, otherwise every knife would be as thick as possible and have as thin edge angles as possible. The relationship is there, the only question is how to illustrate it.

There's just no real relationship between edge retention and blade cross section area unless You force this artificial constraint of constant bevel height.

As I already explained, there is a real relationship between edge retention and cross section: the contact force of the edge on the material. In order to illustrate this relationship in terms of tougness, I showed the effect of making the entire blade's cross section proportionally thinner. That way we don't have to worry about the dynamics of changing the toughness of part of the blade but not the rest. That this choice is done for convenience does not make the relationship unreal.

Additionally this ignores all other blade dimensions like height and secondary bevel angle which actually influence the cross section area and thus toughness.

Yes that's precisely the point. We want to ignore that by talking about proportional changes.

This just makes this extrapolation misleading as it implies choosing a thinner knife will provide the user with better edge retention. It won't. Sharpening at a shallower angle will.

It would only be misleading if you only looked at the image and ignored all of the text explaining the image. Which would be silly.

It would be much more informative to plot edge retention over edge angle - to help compare steels at their lowest sustainable edge angles

That's already been done, I wanted to do something different.

[horzuff]

Don't You think that's just forcing a relationship that's just not there? You can increase edge retention without decreasing toughness by decreasing edge angle while leaving thickness alone, or increase toughness without sacrificing edge retention by keeping the edge angle and increasing thickness.

Decreasing edge angle does decrease toughness, and increasing thickness does decrease edge retention or at least cutting ability, otherwise every knife would be as thick as possible and have as thin edge angles as possible. The relationship is there, the only question is how to illustrate it.

You're mixing and matching parameters to conform with Your narrative. Blade cross section is blade toughness, edge angle is edge toughness (though not stability). And cutting ability is not part of the discussion. That's the thing, the relationship is not there without the weird "constant bevel height and no secondary bevel" assumption.

There's just no real relationship between edge retention and blade cross section area unless You force this artificial constraint of constant bevel height.

As I already explained, there is a real relationship between edge retention and cross section: the contact force of the edge on the material. In order to illustrate this relationship in terms of tougness, I showed the effect of making the entire blade's cross section proportionally thinner. That way we don't have to worry about the dynamics of changing the toughness of part of the blade but not the rest. That this choice is done for convenience does not make the relationship unreal.

The effect of cross section on edge retention is a couple % compared to effect of angle being two orders of magnitude higher. Without the artrificial restraint of bevel height the relationship You're presenting IS ABSENT.

Additionally this ignores all other blade dimensions like height and secondary bevel angle which actually influence the cross section area and thus toughness.

Yes that's precisely the point. We want to ignore that by talking about proportional changes.

But this proportional change isn't present in reality. You just created it artificially

This just makes this extrapolation misleading as it implies choosing a thinner knife will provide the user with better edge retention. It won't. Sharpening at a shallower angle will.

It would only be misleading if you only looked at the image and ignored all of the text explaining the image. Which would be silly.

But You just posted the graph without context in another thread. And most people will just look at the graph and take it for granted because it does imply that thickness affects edge retention directly without any disclaimers...

[Synov]

You're mixing and matching parameters to conform with Your narrative. Blade cross section is blade toughness, edge angle is edge toughness (though not stability).

I'm talking about toughness, which is just the resistance to fracturing. That applies to the entire knife.

And cutting ability is not part of the discussion. That's the thing, the relationship is not there without the weird "constant bevel height and no secondary bevel" assumption.

Well if you want to talk about a knife so thick that it can't cut then I don't see the point. A knife that can't cut has 0 edge retention. Again, you're confusing a choice of mathematical convenience for displaying the data with the relationship in the data. The relationship is there, you're just being obtuse

The effect of cross section on edge retention is a couple % compared to effect of angle being two orders of magnitude higher.

You're begging the question by assuming they are separate effects that can be compared when they are the same effect. Here's a force diagram:



What do you think happens when you increase the edge angle? The bevel thickness increases and the pressure at the edge decreases. I don't know how to make it any clearer. Let's try it this way, why do you think edge angle affects edge retention?

Without the artrificial restraint of bevel height the relationship You're presenting IS ABSENT.

No you have it completely backwards. Without that restraint, the relationship still exists but it's harder to visualize in a chart!

But this proportional change isn't present in reality. You just created it artificially

It is in reality if you make the blade proportionally thinner...

But You just posted the graph without context in another thread. And most people will just look at the graph and take it for granted because it does imply that thickness affects edge retention directly without any disclaimers...

Without context? No. I said make a tough sword out of a thick piece of steel and make a straight razor out of a thin piece of steel. Seems clear enough but for some reason you can't accept it.

[horzuff]

And cutting ability is not part of the discussion. That's the thing, the relationship is not there without the weird "constant bevel height and no secondary bevel" assumption.

Well if you want to talk about a knife so thick that it can't cut then I don't see the point. A knife that can't cut has 0 edge retention. Again, you're confusing a choice of mathematical convenience for displaying the data with the relationship in the data. The relationship is there, you're just being obtuse

Now You're just twisting what I said... Starting to think this discussion is pointless

The effect of cross section on edge retention is a couple % compared to effect of angle being two orders of magnitude higher.

You're begging the question by assuming they are separate effects that can be compared when they are the same effect. Here's a force diagram:



What do you think happens when you increase the edge angle? The bevel thickness increases and the pressure at the edge decreases. I don't know how to make it any clearer. Let's try it this way, why do you think edge angle affects edge retention?

Why would edge angle change bevel thickness? That's the thing, it doesn't. Not unless You keep forcing those weird constraints of Yours. As for diagrams (which Yours is about splitting force in a push cut so more along the lines of sharpness, not slicing edge retention), here's one from KnifeSteelNerds which shows influence of stock thickness vs edge angle on edge retention in reality and not Your weird make-believe-land...

(source https://knifesteelnerds.com/2018/06/18/ ... retention/)

Without the artrificial restraint of bevel height the relationship You're presenting IS ABSENT.

No you have it completely backwards. Without that restraint, the relationship still exists but it's harder to visualize in a chart!

But this proportional change isn't present in reality. You just created it artificially

It is in reality if you make the blade proportionally thinner...

As shown in the graph from KSN, no it doesn't, definitely not at the magnitude You imply

But You just posted the graph without context in another thread. And most people will just look at the graph and take it for granted because it does imply that thickness affects edge retention directly without any disclaimers...

Without context? No. I said make a tough sword out of a thick piece of steel and make a straight razor out of a thin piece of steel. Seems clear enough but for some reason you can't accept it.

Make that same sword but set the edge at a lower angle and You still have almost the same edge retention as the thin piece. That's the problem here. Blade thickness has negligible impact on edge retention compared to edge angle, period. Edge angle is not tied to blade thickness, another period.

[Synov]

Why would edge angle change bevel thickness? That's the thing, it doesn't.

Bevel Thickness = 2sin(Edge Angle/2)*Bevel Height

They are directly related.

As for diagrams (which Yours is about splitting force in a push cut so more along the lines of sharpness, not slicing edge retention)

No, it applies to both push cut and slicing. Both are applying a force downward.

here's one from KnifeSteelNerds which shows influence of stock thickness vs edge angle on edge retention in reality and not Your weird make-believe-land...

(source https://knifesteelnerds.com/2018/06/18/ ... retention/)

That's comparing two knives with the same edge angle but different bevel thicknesses AND different bevel heights. That's the only way to make the knives have the same edge angle. How is one more real than the other? How is an analysis that doesn't change the edge angle relevant to my analysis that does change the edge angle? I don't think you understand what you're arguing against. Basically you're complaining that I did an analysis different from what other people have done. OK.

Make that same sword but set the edge at a lower angle and You still have almost the same edge retention as the thin piece.

But how does that lower edge angle affect toughness? If you claim it doesn't affect toughness, why don't we just put a thin edge on everything? Again, you keep trying to limit the analysis to one parameter when it's about multiple.

Blade thickness has negligible impact on edge retention compared to edge angle, period. Edge angle is not tied to blade thickness, another period.

Only if you change bevel height to keep edge angle the same, which is just as arbitrary a choice as keeping bevel height the same and doesn't change my point. You destroyed your argument by presenting an equally valid alternative analysis.

And you failed to answer my question: why do you think edge angle affects edge retention?

[Mage7]

Why would edge angle change bevel thickness?

Well, who knows why but the basic laws of geometry, and specifically trigonometry, dictate that is so.

It might help to realize that a V-bevel can be considered as two right-triangles put up against one another.



Picture that this right-triangle is one half of your edge. The hypotenuse is the bevel face, the opposite is the line that would intersect the blade cross-sectionally at the bevel shoulder, and the adjacent is aligned to the center-line axis from the edge apex to spine.

By "bevel thickness" I'm not sure if you mean the length of the hypotenuse, or the size of the gap between the hypotenuse and the adjacent. Either way, changing the "edge angle", which is the angle between the hypotenuse and adjacent, must result in changes to either the adjacent or the opposite. If you keep the opposite length the same, changing the angle of the hypotenuse will change the length of the adjacent; if you keep the adjacent the same, changing the angle of the hypotenuse will change the length of the opposite. If you keep the length of the hypotenuse the same, but increase the length of the opposite, then unless you allow the angle of the hypotenuse to change then the length of the opposite must.

Regardless of the primary blade grind angle, the thickness of the blade where the edge bevel is ground on dictates the length of the opposite. It doesn't matter how thick the blade is at the spine, so whether it is ground at an angle or a zero grind like a Scandi doesn't actually matter, since all of these same trigonometric principles apply. As a matter of fact, we can easily calculate the thickness of stock at the spine given the "thickness behind the edge" which is just the length of both 'opposite' sides, and given the angle of the primary blade grind. Similarly we could calculate the angle of the blade grind from knowing those dimensions too.

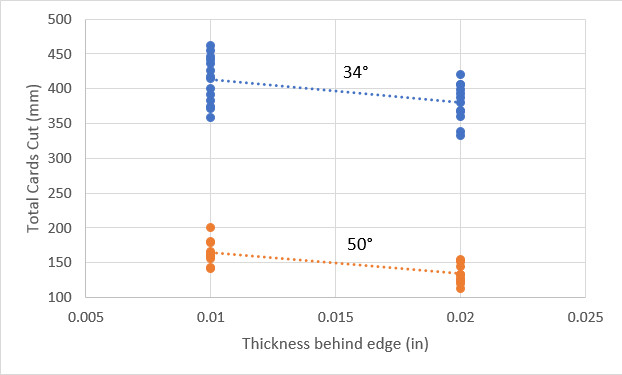
Let's consider the KSN graph you posted...


(source https://knifesteelnerds.com/2018/06/18/ ... retention/)

Forget about the thickness "behind the edge". How about 1mm up from the edge? After all, the CATRA test is cutting 1mm thick cards, so the depth that the edge apex is cutting into is 1mm right? Plus, we don't even know how large the bevel height is to know what "behind the edge" means in this context. For all we know, the actual height of the edge from apex bevel shoulder could be more or less than 1mm.

If we assume it's 1mm, and the card stock is 1mm, how much do you think each bevel is pushing the material apart?

At 34 degrees, 1mm into a card, the thickness of the edge can be calculated as so:

2 * 1 * tan( 34 * pi / 360 ) = 0.611 mm (0.024 in)

At 50 degrees, 1mm into a card, the thickness of the edge can be calculated as so:

2 * 1 * tan( 50 * pi / 360 ) = 0.932 mm (0.036 in)

Obviously, the thicknesses provided are less than what's calculated here, indicating that the bevels are actually less than 1mm high. But if we consider halfway into the cardstock instead, i.e. .5mm then the thicknesses are .012" and 0.18" for the 34 and 50 degree edges, respectively.

The article does indeed show edge angle affecting edge retention to a far greater degree even at equal thickness...



...but it's important to note Larrin's remarks regarding thickness.

Effect of Thickness Behind the Edge

Half of the knives were ground to a thickness of 0.010″ and half to 0.020″ prior to sharpening the final edge. Because the knives were ground by hand there was some variation in thickness both between the knives and along the edge of an individual knife. However, these variations were not recorded. Thinner edges, regardless of final edge angle, did have a small advantage in edge retention, as shown in the figure below. This is consistent with previous studies using a fixed angle but different edge thickness [4].

Conclusions and Further Testing



The figure above is the calculated “relative contribution” to a regression model in terms of impact on R2, a statistical measure of how well a model fits experimental data. The relative contribution was calculated by Minitab. From this study it should be apparent that lower edge angles lead to superior cutting performance. PM vs ingot, cryo, and edge finish appear to be minor factors; Minitab analysis seems to put the contribution to edge retention solely on hardness rather than the PM/ingot difference. Hardness and edge thickness have less effect than edge angle but are still important.It may be interesting to compare a steel with lower carbide volume between its ingot and PM version to see if any difference is perceptible between those. It would also be a good study to look at another type of sharpening stones to see if it was indeed an effect of diamond plate sharpening that led to the peak behavior at 600 grit. I would also like to compare a wider range of edge thicknesses and hardness to get a better idea of those effects since they were over a narrow range in this study. More tests with different types of cryogenic processing would also be interesting. In future articles on edge retention I will compare CATRA testing with other reported edge retention tests, and also cover CATRA testing of different steels with (hopefully) consistent edge angle and sharpening finishes to see what steels are best for edge retention.

My emphasis in bold.

Indeed, if you look at the data table, the "narrow range" is literally only between 0.1" and 0.2" without any greater definition than one tenth of an inch. That's really kind of a dearth of data to make a firm conclusion about how thickness affects edge retention from. It's fair to say edge angle greatly influences it, sure, but to conclude from this data that edge thickness does not is kind of trying to derive a positive proof from a negative. Just because this study didn't show that thickness doesn't have a great influence, doesn't mean it does not, just that it didn't have the data to support that conclusion. On the other hand it did show a minimal influence in greater edge retention so there's more reason to speculate it could have a greater effect than realized than to assert it has only a minor influence.

There's more reason to explore how thickness influences edge retention further than there is reason to assume its influence is negligible.

Also when it comes to the mechanical forces at play...

It's a bit of a misconception that slicing cuts rely on a separate set of mechanical functions than push cuts. There are of course additional forces at play with a slicing motion, but otherwise even while a knife edge is slicing, it is still functioning as a wedge in the same way that it functions as a wedge during a push cut. The only difference is adding lateral movement, but is still fundamentally a wedge.

Which I point out because another unspoken benefit of constraining the bevel height to a specific dimension is that it will introduce a control for the variable of surface area. The bevel faces will be acted upon by compression and friction while displacing the material being cut, and so if you constrain the bevel height to one dimension then you're also ensuring that the surface area the material being cut acts upon doesn't change.

But that's besides the point that the bevel height has as much to do with what is actually mechanically influencing the cut as much as the edge angle, and both things are actually interdependent components of a larger system. If anything, the edge angle is actually a greater abstraction than specifying bevel height, since the edge angle is only meaningful with an implied relation to the centerline of the edge apex.

Take a look at these charts I let ChatGPT generate...

This is based on a blade if it had a constant bevel height of 10mm, with either the stock thickness (where the edge bevel begins) or the edge angle being the varying factor.

In this context the "gap" is the distance from either bevel face to the other at 1mm up from the edge apex, which would be the depth of the cut into a CATRA test card.

So in other words the "gap" is the thickness of the blade at its widest displacement of the CATRA card as it cuts into it.

As you can see, controlling for that thickness via stock thickness or edge angle while keeping the bevel height constant are both viable approaches. The gap will increase or decrease by ~0.1mm per 1mm of stock thickness, or by about ~0.035mm per 1 degree.

Now, as far as how this all would differ in actual testing and how that would be advantageous... Again, it controls for the surface area of the bevel faces and thus the forces acting upon them, and it also allows for greater resolution if someone did want to test how different thicknesses influenced edge retention because it's much, much easier to precisely grind the cross-sectional thickness of a blade within tolerances of +/- .025mm (.001in) than it is to precisely grind angles at even +/- 1 degree.


All of that is just in regards to the validity and advantage--and perhaps the necessity--of constraining bevel height in regard to edge geometry, however. I think there's still a lot to question about how toughness might actually directly translate to better edge retention that would require that testing to be done.

I can't help but feel like how well toughness values derived from charpy testing will really translate into higher edge retention for two reasons. Firstly is the question of how much a thinner edge will actually contribute to higher edge retention that's already been raised, but I'm willing to assume that it would and we just don't have empirical data to show that.

The bigger elephant in the room, in my opinion, is the question of edge stability. Even if we can safely assume that reducing the cross-sectional thickness of the edge will greatly improve edge retention, at what point will its inability to maintain structural integrity fail? For all we really know, it could even fail before the reduction in thickness can substantially increase edge retention in the first place.

If we can't definitively say, "A thinner edge will cut longer, and a tougher edge can be thinner," then the numbers working in a mathematical relationship doesn't really matter much. Since, as it's been mentioned, stability is influenced by hardness, toughness and edge geometry--and since toughness and hardness are diametrically opposed--the only way I think this could work is if the cross-sectional thickness of the edge could be reduced to extremely small levels while the structural integrity of the edge is fortified fortified by geometry. In other words, very obtuse edge angles, at very extreme thinness. Realistically, this is already how most metal-cutting tools (twist drill bits, cutoff and facing bits, etc.) achieve stability, but unfortunately that then leaves them to rely upon significant force to cut.

[horzuff]

I feel like I'm talking with someone from some bizzaro world . I mean, does Your knife get thicker/thinner when You change the edge angle?

Don't have enough patience to keep pointing out all the unnatural assumptions and and mental acrobatics You guys make to force the idea...

I would understand If You tried to approximate edge toughness depending on edge angle, but that by itself is only part of the story and doesn't define stability/durability fully. But at least You would have some actual relationship of characteristics at hand.

And that would still be completely unrelated to blade thickness. Which only influences knife toughness, not edge performance.

I mean, do You claim B will have meaningfully higher edge retention than A? Angle is the same, A's thickness is twice that of B.

And conversely, will D have better edge retention than C? D is half as thick but twice the edge angle of C.

What about toughness in these scenarios?

[Synov]

I feel like I'm talking with someone from some bizzaro world . I mean, does Your knife get thicker/thinner when You change the edge angle?

Yes, specifically the bevel thickness. But even if we ignore that, the intent of your question is silly. Does the bevel height necessarily change when the thickness changes? Oh so how can you POSSIBLY link to an analysis that has both changing?

Don't have enough patience to keep pointing out all the unnatural assumptions and and mental acrobatics You guys make to force the idea...

You haven't pointed out anything unnatural. You linked to an analysis comparing C to D but for some reason I can't compare C to B. Makes no sense.

I would understand If You tried to approximate edge toughness depending on edge angle, but that by itself is only part of the story and doesn't define stability/durability fully. But at least You would have some actual relationship of characteristics at hand.

I have no data on edge toughness. There is an actual relationship, mathematically proven to you. You're just unwilling to accept that someone could do an analysis different from one you're already familiar with. You have no actual argument, just claims that contradict proof.

And that would still be completely unrelated to blade thickness. Which only influences knife toughness, not edge performance.

You already provided an analysis showing that thickness behind the edge does have a small influence on edge retention, so I'm not sure why you're saying this.

I mean, do You claim B will have meaningfully higher edge retention than A? Angle is the same, A's thickness is twice that of B.

And conversely, will D have better edge retention than C? D is half as thick but twice the edge angle of C.

Edge Retention will be somewhat higher in both cases. But that has nothing to do with my original claim, which is that B will have higher edge retention and lower toughness than C in a very precise way. Why are your comparisons natural while mine is unnatural?

[Deadboxhero]

A great discussion is being had here, however, I think it's important for us to be more respectful to each other if possible.

We forget our community is a lot smaller than we imagine and we've lost a lot of good people over the past 5 years.


There simply aren't many of us that discuss things at this level of detail, so technically we should all be quite good friends.

Nobody even talks about this stuff at Bladeshow.
A niche within a niche.

I'd like to see this specific topic move more into physical experiments rather than just simulation alone.

Good job guys, it takes patience.

[sal]

Hey Shawn,

Agree with your "let's be friendly here". Thanx for the reminder.

Your opinion on what physical tests would work best?

I've envisioned some type of "90 degree edge squashing" test.

sal

[Deadboxhero]

Hey Shawn,

Your opinion on what physical tests would work best?

I've envisioned some type of "90 degree edge squashing" test.

sal

Sal,

That sounds interesting, do you think you can give us a rough test outline for the idea you have for a 90° edge squashing test?

Sounds like a great way to get the ball rolling.

[sal]

Hi Shawn,

I'll see what I can show to give you an idea of what I'm thinking. At this point, it has only been a thought (Muscle twitches and gland secretions).

I'm pretty busy, but I'll talk to Peter tomorrow. If we get serious about building one, I think it would be valuable to get Larrin involved?

sal